Sistema de numeración
En el primer ciclo de la escuela primaria se privilegia la utilización de los números ante
diversos problemas y en contextos significativos. A su vez, se propician las reflexiones de
los alumnos que les permitirán reconocer regularidades y apoyarse en ellas para producir
e interpretar, comparar y operar con números. Se inicia también el análisis del valor posicional
de las cifras.
En el segundo ciclo los alumnos deben trabajar para ampliar la porción de la serie numérica para leer, escribir y ordenar números. Por otro lado, deberán avanzar sobre la conceptualización del sistema comprendiendo la organización recursiva de los agrupamientos, el rol jugado por la base y el significado de la posición de las cifras. Para avanzar en el análisis del valor posicional es necesario abordar las relaciones multiplicativas subyacentes al sistema: "Mayores conocimientos sobre el sistema de numeración decimal" significa fundamentalmente que los alumnos sean capaces de explicitar las relaciones aritméticas subyacentes a un número (que no se reducen a la descomposición polinómica) y que sean capaces de utilizar la información contenida en la escritura decimal para desarrollar métodos de cálculo, redondeo, aproximación, encuadramiento, etcétera, que les permitan resolver problemas. Un aspecto importante de ese trabajo consiste en que puedan analizar la información que brinda la escritura de un número, según el valor posicional de sus cifras, para resolver una gran variedad de situaciones tales como: resolver cálculos, anticipar el resultado de un cálculo, anticipar restos y cantidad de cifras de un cociente, etc.
El aprendizaje de la numeración en el segundo ciclo de la escuela primaria, entonces, abarca varios tipos de problemas que se ven reflejados en esta progresión: problemas referidos a leer, escribir, comparar y ordenar números, y problemas referidos al análisis del valor posicional de las cifras.
Es muy importante explicitar que la evolución en los niveles de progresión que a continuación se desarrollan podrá aparecer bajo la condición de que los alumnos hayan participado en situaciones sostenidas y sistemáticas de enseñanza para cada clase de problemas.
En el segundo ciclo los alumnos deben trabajar para ampliar la porción de la serie numérica para leer, escribir y ordenar números. Por otro lado, deberán avanzar sobre la conceptualización del sistema comprendiendo la organización recursiva de los agrupamientos, el rol jugado por la base y el significado de la posición de las cifras. Para avanzar en el análisis del valor posicional es necesario abordar las relaciones multiplicativas subyacentes al sistema: "Mayores conocimientos sobre el sistema de numeración decimal" significa fundamentalmente que los alumnos sean capaces de explicitar las relaciones aritméticas subyacentes a un número (que no se reducen a la descomposición polinómica) y que sean capaces de utilizar la información contenida en la escritura decimal para desarrollar métodos de cálculo, redondeo, aproximación, encuadramiento, etcétera, que les permitan resolver problemas. Un aspecto importante de ese trabajo consiste en que puedan analizar la información que brinda la escritura de un número, según el valor posicional de sus cifras, para resolver una gran variedad de situaciones tales como: resolver cálculos, anticipar el resultado de un cálculo, anticipar restos y cantidad de cifras de un cociente, etc.
El aprendizaje de la numeración en el segundo ciclo de la escuela primaria, entonces, abarca varios tipos de problemas que se ven reflejados en esta progresión: problemas referidos a leer, escribir, comparar y ordenar números, y problemas referidos al análisis del valor posicional de las cifras.
Es muy importante explicitar que la evolución en los niveles de progresión que a continuación se desarrollan podrá aparecer bajo la condición de que los alumnos hayan participado en situaciones sostenidas y sistemáticas de enseñanza para cada clase de problemas.
Progresiones de los aprendizajes a lo largo del segundo ciclo
| Primer ciclo | Nivel I | Nivel II | |||||||||||||||
|
Lee, escribe y ordena números hasta aproximadamente
10.000. En situaciones colectivas explora las regularidades en la serie oral y la serie escrita, intercambiando ideas acerca del nombre, la escritura y la comparación de números de diversa cantidad de cifras. |
Lee, escribe y ordena números hasta aproximadamente
1.000.000:
|
Lee, escribe y ordena números sin restricciones en la cantidad
de cifras. Lee y escribe números utilizando como referente unitario los miles o los millones. Por ejemplo:
Decidí qué número es 3 millones y medio, y explicá cómo te diste cuenta:
|
|||||||||||||||
|
Resuelve problemas que exijan usar escalas ascendentes y
descendentes de 100 en 100, 200 en 200, de 500 en 500
y de 1.000 en 1.000.
Por ejemplo:
En un bosque hay 1.200 árboles. Quieren aumentar la cantidad y cada año plantan 200 árboles. ¿Cuántos árboles se supone que habrá en los próximos 5 años? |
Resuelve problemas que exijan usar escalas ascendentes y descendentes de 500 en 500, de 1.000 en 1.000, de 10.000 en 10.000. | ||||||||||||||||
|
Determina la ubicación de números en una recta numérica, en
la que ya se han señalado las subdivisiones correspondientes
y se dan distintas informaciones numéricas:
Por ejemplo:
Esta es una parte de una recta:
|
Determina la ubicación de números en una recta numérica en
la que solo se informa el intervalo entre dos números.
Por ejemplo:
En esta recta ubicá de la manera más precisa posible los siguientes números: 200.000, 600.000, 800.000, 850.000. Construye una recta numérica para ubicar diferentes números tomando decisiones sobre la escala a utilizar.
Por ejemplo:
Elegí para cada recta, una graduación que te permita ubicar, aproximadamente, los números que se indican.
|
||||||||||||||||
|
Resuelve problemas que requieran reconocer y analizar el
valor posicional de las cifras con números hasta 10.000.
Por ejemplo:
Resuelve problemas que requieren poner en juego las relaciones entre las diferentes posiciones de una cifra (determinando que en 100 hay 10 de 10; o en 1.000 hay 10 de 100).
Por ejemplo:
|
Resuelve problemas que requieren reconocer y analizar el valor
posicional de las cifras, poniendo en juego las relaciones
contiguas entre ellas (10 de 100 equivalen a 1 de mil; 10 de
1.000 equivalen a 1 de 10.000, etcétera) a partir de:
|
Resuelve problemas que requieren reconocer y analizar el valor
posicional de las cifras, poniendo en juego las relaciones
entre diferentes posiciones de las cifras y no solamente las
contiguas (100 de 100 equivalen a 10 de mil; 1.000 de 1.000
equivalen a 1 de 1.000.000, etcétera) a partir de:
|
|||||||||||||||
- Tabla en formato PDF Descargar »
Actividades para relevar los aprendizajes
Se incluyen aquí algunos ejemplos de problemas que podrían ser útiles a la hora de recabar información sobre el estado de conocimientos de los alumnos en relación con el eje Sistema de Numeración. En el trabajo cotidiano en el aula, observar su desempeño mientras resuelven los problemas que se les plantean, analizar el tipo de intervenciones y preguntas que hacen y los comentarios o explicaciones que pueden dar de su trabajo, da indicadores para conocer qué saben. Sin embargo, se hace necesario también plantear momentos específicos de trabajo individual que permitan mirar más detenidamente la producción de cada uno. Las situaciones propuestas a continuación responden a este propósito.
Ejemplos de situaciones didácticas e intervenciones docentes
Intervenciones de enseñanza
Al proponer situaciones de escritura y lectura de números, el tipo de números propuestos
dependerá del rango numérico que se esté trabajando en particular.
En situaciones grupales es posible presentar la opción de leer o escribir números de mayor cantidad de cifras de las que se estén trabajando en particular para ayudar a sistematizar algunas regularidades, sin el objetivo, en ese momento, de asegurar el dominio de la lectura y escritura por parte de los niños. Por ejemplo, en un grado se puede estar trabajando específicamente con números de 5 o 6 cifras para sistematizar su lectura y escritura, y, sin embargo, proponer otras situaciones de discusión sobre números mayores como: si este (31.000.000) es treinta y un millones, cómo se escribirá el treinta y un millones cuatrocientos, con la intención de reparar en información que da la numeración oral para la escritura y las regularidades con respecto a la cantidad de cifras. En este caso, se podría analizar que como el nombre de ambos números empieza igual, su escritura también, o sea comenzará con “31”, y por otro lado, ambos deberán tener ocho cifras.
En el documento Progresiones de los aprendizajes. Primer ciclo. Matemática se señala que la correspondencia entre el nombre de los números y su escritura no es directa: a partir del nombre no se puede deducir directamente la escritura ni viceversa. Esta falta de correspondencia entre ambos tipos de representación da lugar a ciertos errores que los niños producen. No es tarea fácil para un niño descubrir qué es lo que está oculto en la numeración hablada y qué es lo que está oculto en la numeración escrita, se hace necesario reconocer cuáles son las informaciones provistas por la numeración hablada que resulta pertinente aplicar a la numeración escrita y cuáles no (por ejemplo, en el nombre de los números no se observa explícitamente el o los ceros que puede incluir su escritura, el nombre del número explicita la potencia de la base que no se escribe pues está implícita en la posición de cada cifra, en la escritura se usan puntos que no tienen referencia en la numeración oral, etcétera). Es importante tener en cuenta que, en segundo ciclo, al avanzar hacia números mayores, esta relación entre el nombre y la escritura se complejiza:
Teniendo en cuenta lo señalado, es posible que al leer números el niño:
A la vez, es posible que al escribir números:
Como se puede observar en los ejemplos que siguen, a la hora de escribir números los niños pueden producir escrituras convencionales en algunos casos, incluso en números mayores y en otros, aunque sean menores, no. La cantidad de cifras no es necesariamente lo que hace que un número resulte más complejo de leer o escribir que otro. En ese sentido, la presencia de ceros intermedios o si se trata de números redondos o no, son variables centrales a tener en cuenta.
Por ejemplo, Milagros, de 4º grado, escribe:
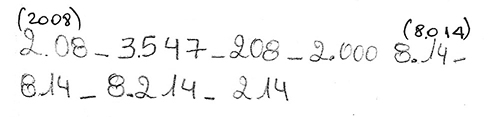
Frente a esta escritura, la docente le pregunta si es posible que dos números diferentes (haciendo referencia al dos mil ocho y al doscientos ocho) puedan escribirse de la misma manera. Milagros responde que no están iguales esas escrituras, pues una tiene el punto (2.08) y la otra no (208).
Ella, como Franco en el ejemplo siguiente, pueden escribir convencionalmente números redondos de cuatro o cinco cifras o números de cuatro o cinco cifras sin ceros intermedios, pero producen errores en números que incluyen ceros intermedios y le asignan al punto el valor de “mil”, sin tener en cuenta la cantidad de cifras.

En ambos casos, el docente puede hacer referencia a la escritura y el nombre de los números redondos como apoyo para revisar esas escrituras que resultaron erróneas. Por ejemplo: Si el nueve mil se escribe así (9.000) con cuatro cifras, ¿cuántas cifras tendrá el nueve mil cinco? ¿Puede ser que tenga solo dos cifras?; si este es el cuarenta y cinco mil (45.000), ¿cómo será el cuarenta y siete mil? ¿Puede ser que tenga solo dos cifras? ¿Menos cifras que el cinco mil setecientos treinta y nueve que escribiste arriba? Restituir el nombre y la escritura correcta de los números redondos y hacer referencia a la cantidad de cifras es una ayuda muy importante para que los niños puedan controlar sus propias escrituras. En ambos casos también, la explicitación de que el punto no alcanza para que un número sea “de los miles” y que lo central es la cantidad de cifras, puede permitir que el niño revise sus escrituras.
Algunas intervenciones que un maestro puede realizar para ayudar a un niño en particular a escribir o leer números son:
Como intervención general en situaciones grupales puede resultar pertinente proponer la reflexión en torno a las relaciones entre la numeración oral y la numeración escrita. Es importante sistematizar las conclusiones que se deriven de esas discusiones en carteles para el aula y para los cuadernos a los que poder referir luego en todos los casos en los que sea necesario.
Por ejemplo, dejar registro sobre:
En situaciones grupales es posible presentar la opción de leer o escribir números de mayor cantidad de cifras de las que se estén trabajando en particular para ayudar a sistematizar algunas regularidades, sin el objetivo, en ese momento, de asegurar el dominio de la lectura y escritura por parte de los niños. Por ejemplo, en un grado se puede estar trabajando específicamente con números de 5 o 6 cifras para sistematizar su lectura y escritura, y, sin embargo, proponer otras situaciones de discusión sobre números mayores como: si este (31.000.000) es treinta y un millones, cómo se escribirá el treinta y un millones cuatrocientos, con la intención de reparar en información que da la numeración oral para la escritura y las regularidades con respecto a la cantidad de cifras. En este caso, se podría analizar que como el nombre de ambos números empieza igual, su escritura también, o sea comenzará con “31”, y por otro lado, ambos deberán tener ocho cifras.
En el documento Progresiones de los aprendizajes. Primer ciclo. Matemática se señala que la correspondencia entre el nombre de los números y su escritura no es directa: a partir del nombre no se puede deducir directamente la escritura ni viceversa. Esta falta de correspondencia entre ambos tipos de representación da lugar a ciertos errores que los niños producen. No es tarea fácil para un niño descubrir qué es lo que está oculto en la numeración hablada y qué es lo que está oculto en la numeración escrita, se hace necesario reconocer cuáles son las informaciones provistas por la numeración hablada que resulta pertinente aplicar a la numeración escrita y cuáles no (por ejemplo, en el nombre de los números no se observa explícitamente el o los ceros que puede incluir su escritura, el nombre del número explicita la potencia de la base que no se escribe pues está implícita en la posición de cada cifra, en la escritura se usan puntos que no tienen referencia en la numeración oral, etcétera). Es importante tener en cuenta que, en segundo ciclo, al avanzar hacia números mayores, esta relación entre el nombre y la escritura se complejiza:
- En los números de hasta 4 cifras, a cada una de las potencias de diez le corresponde un
nuevo nombre:
- Los puntos no tienen referencia en la lengua oral, pero ayudan a interpretar escrituras numéricas. Los niños suelen producir sus propias interpretaciones del uso y función de los puntos en la escritura de los números.
Teniendo en cuenta lo señalado, es posible que al leer números el niño:
- Genere nombres no convencionales, en particular en números que tienen puntos en su escritura. Por ejemplo, a 3.147.456 lo lee como “tres mil ciento cuarenta y siete mil cuatrocientos cincuenta y seis”.
- Cambie el rango al que pertenecen. Por ejemplo, a 103.024 lo lee como “diez mil trescientos veinticuatro”.
- Asigne a cada punto un nombre de una potencia cada vez mayor. Por ejemplo: a 1.234.340.230 lo lee como “un billón, doscientos treinta y cuatro millones trescientos cuarenta mil doscientos treinta”.
A la vez, es posible que al escribir números:
- Produzca escrituras que reflejan todo lo que se enuncia en la emisión oral. Por ejemplo, para 3.058 y 2.080, un alumno escribe:
- Produzca escrituras en el rango de los “miles” o “millones” omitiendo los ceros intermedios. Por ejemplo: un alumno escribe “18.14” para dieciocho mil catorce.
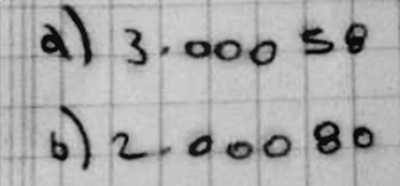
Como se puede observar en los ejemplos que siguen, a la hora de escribir números los niños pueden producir escrituras convencionales en algunos casos, incluso en números mayores y en otros, aunque sean menores, no. La cantidad de cifras no es necesariamente lo que hace que un número resulte más complejo de leer o escribir que otro. En ese sentido, la presencia de ceros intermedios o si se trata de números redondos o no, son variables centrales a tener en cuenta.
Por ejemplo, Milagros, de 4º grado, escribe:
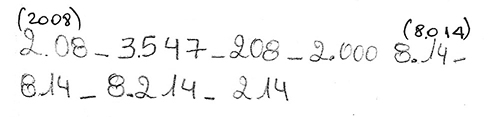
Frente a esta escritura, la docente le pregunta si es posible que dos números diferentes (haciendo referencia al dos mil ocho y al doscientos ocho) puedan escribirse de la misma manera. Milagros responde que no están iguales esas escrituras, pues una tiene el punto (2.08) y la otra no (208).
Ella, como Franco en el ejemplo siguiente, pueden escribir convencionalmente números redondos de cuatro o cinco cifras o números de cuatro o cinco cifras sin ceros intermedios, pero producen errores en números que incluyen ceros intermedios y le asignan al punto el valor de “mil”, sin tener en cuenta la cantidad de cifras.

En ambos casos, el docente puede hacer referencia a la escritura y el nombre de los números redondos como apoyo para revisar esas escrituras que resultaron erróneas. Por ejemplo: Si el nueve mil se escribe así (9.000) con cuatro cifras, ¿cuántas cifras tendrá el nueve mil cinco? ¿Puede ser que tenga solo dos cifras?; si este es el cuarenta y cinco mil (45.000), ¿cómo será el cuarenta y siete mil? ¿Puede ser que tenga solo dos cifras? ¿Menos cifras que el cinco mil setecientos treinta y nueve que escribiste arriba? Restituir el nombre y la escritura correcta de los números redondos y hacer referencia a la cantidad de cifras es una ayuda muy importante para que los niños puedan controlar sus propias escrituras. En ambos casos también, la explicitación de que el punto no alcanza para que un número sea “de los miles” y que lo central es la cantidad de cifras, puede permitir que el niño revise sus escrituras.
Algunas intervenciones que un maestro puede realizar para ayudar a un niño en particular a escribir o leer números son:
- Remitir a carteles informativos que estén pegados en las paredes del aula o en las carpetas (resultan esenciales para que los alumnos recuperen discusiones anteriores).
- Pedirle al niño que anticipe, antes de escribir, la cantidad de cifras que deberá tener un número determinado. Por ejemplo: hacerlo notar que, si el doscientos cuarenta mil quinientos es de los cien miles, entonces tendrá 6 cifras.
- Proveer el nombre correcto de un número y su escritura, para que sirva de apoyo para la escritura de otro. Por ejemplo: Este número (20.020) es el veinte mil veinte, ¿cómo se llamará este número (20.040)?
Como intervención general en situaciones grupales puede resultar pertinente proponer la reflexión en torno a las relaciones entre la numeración oral y la numeración escrita. Es importante sistematizar las conclusiones que se deriven de esas discusiones en carteles para el aula y para los cuadernos a los que poder referir luego en todos los casos en los que sea necesario.
Por ejemplo, dejar registro sobre:
- La escritura y el nombre de los números redondos que corresponden al rango numérico que se está trabajando. Por ejemplo:
- El apoyo que ofrecen los números redondos para escribir otros:
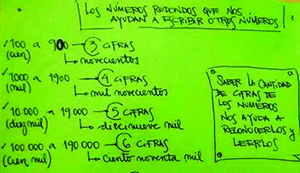
- Las regularidades referidas a la cantidad de cifras de cada orden:
- El rol del punto en los números escritos, ya que muchos alumnos consideran que con la presencia del punto alcanza para que un número sea, por ejemplo, de los miles.

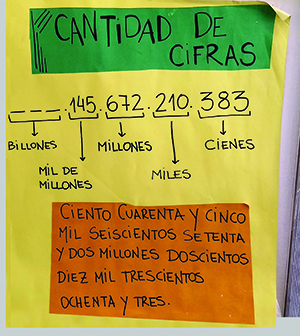


En el segundo ciclo los niños deben avanzar y profundizar su comprensión sobre el funcionamiento
del sistema de numeración. Esto implica comprender no solamente qué valor
tiene cada cifra según su posición en el número, sino comprender además la organización
recursiva de los agrupamientos: cada diez elementos de un orden se conforma un elemento
del orden superior siguiente (con diez decenas se conforma una centena, con diez centenas
se conforma una unidad de mil, etcétera). En ese sentido, el avance implica que, por ejemplo,
los niños puedan reconocer que en el número 4.567 hay 45 centenas pues 4 unidades
de mil son 40 centenas. Esta recursividad de los agrupamientos resulta más sencilla de
identificar entre posiciones contiguas de las cifras, pero hay que reconocerla también entre
posiciones no contiguas. Por ejemplo, en el 3.036 hay 303 decenas porque 3 unidades de
mil son 300 decenas. Comprender el sistema en términos de “unidad, decena, centena,
unidad de mil, etcétera” implica comprender este aspecto multiplicativo de nuestro sistema
de numeración.
Se busca además que los niños sean capaces de utilizar la información contenida en la escritura decimal para desarrollar métodos de cálculo exacto o aproximado. Es importante que el docente explicite a los niños que es posible utilizar esa información para resolver cálculos pues no necesariamente todos los alumnos establecen ese vínculo por sí solos.
A continuación, se retoman las intervenciones propuestas en el documento Progresiones de los aprendizajes. Primer ciclo. Matemática para el trabajo con sistema de numeración, dado que pueden resultar también pertinentes con niños del segundo ciclo ajustándolas en función de los nuevos rangos numéricos:
En el segundo ciclo es necesario promover, como se señaló, la profundización en el análisis del valor posicional en cuanto a las relaciones entre las distintas posiciones de las cifras en un número: 10 de 10 forman uno de 100; luego también 10 de 100 uno de 1.000, 10 de 1.000 forman 10.000, etcétera, primero entre posiciones contiguas (decenas con centenas; centenas con unidades de mil, etcétera) y luego entre posiciones no contiguas (decenas con unidades de mil, etcétera). Si frente a la situación de tener que determinar cuántos billetes de 100 y monedas de 1 se necesitan para obtener $3.436, un niño no encuentra una estrategia de resolución, es posible preguntarle si se puede armar $1.000 con billetes de $100 (en el caso de que haya en el aula conclusiones escritas sobre esa relación, será valioso remitirlo a ellas). A partir de allí avanzar preguntando: Si con 10 de 100 tengo 1.000, ¿cuánto tendré con 20 billetes de $100?, ¿y con 30? Escribir junto con él esas relaciones que van surgiendo permite sistematizar cierta regularidad (10 de 100 “hacen” 1.000; 20 “hacen” 2.000; etcétera) y dejar esa información disponible para poder recurrir a ella en otras situaciones.
Vincular la recursividad de agrupamientos de a 10 con la multiplicación por 10, 100 y 1.000 permite poner en primer plano el aspecto multiplicativo del sistema de numeración. Por ejemplo:

Es necesario tener en cuenta que cuanto mayor sea el grado de generalidad que se solicite en las formulaciones, la complejidad se incrementa para los niños. Por eso es necesario abordar este contenido en instancias de trabajo colectivo antes de exigir individualmente la disponibilidad de estas conclusiones. Será necesario un progresivo trabajo de contextualizaciones y descontextualizaciones para ir hacia formulaciones más generales.
Hay otras situaciones que permiten avanzar sobre el conocimiento del valor posicional de las cifras. Por ejemplo, problemas del tipo: ¿Cuántos paquetes de 100 ganchitos se pueden armar con 432? ¿Sobran algunos? ¿Cuántos? En este caso, es posible que muchos niños planteen algunos cálculos de división o de multiplicación. Lo central será discutir si es posible responder esa pregunta analizando la información que provee la escritura del número 432 sin necesidad de resolver ningún cálculo. Así la división 432 : 100 podrá ser respondida a partir de utilizar la información que dan las cifras del número. Incorporar este tipo de problemas permite avanzar en otro contexto para profundizar el análisis de las propiedades del sistema de numeración y su relación con la división por la unidad seguida de cero: Si las cifras representan agrupamientos de 10, 100, 1.000, etcétera, será posible, entonces, usar esa información para responder preguntas sobre ese tipo de agrupamientos. En este caso en particular, si en el 432 hay 4 de 100, entonces será posible concluir que se pueden armar 4 paquetes y van a sobrar 32, que no llegan a armar paquetes de 100. Se trata, en definitiva, de hacer confluir la división por 10, 100, 1.000, etcétera y las propiedades de nuestro sistema de numeración. En las discusiones será importante que se haga explícita esa relación. Así, el avance tendrá que ver luego con la posibilidad de descontextualizar esas relaciones, respondiendo estas preguntas: ¿Y cómo podemos saber cuánto da el cociente y el resto de cualquier número dividido 10, 100 o 1.000, sin hacer la cuenta? ¿Es posible? ¿Cómo? Esas formulaciones generales surgidas también pueden volcarse en carteles o textos para las carpetas.
El trabajo con otros sistemas de numeración antiguos, posicionales y no posicionales (la numeración romana, egipcia, china, etcétera) es también una oportunidad para reflexionar sobre las propiedades de nuestro sistema de escritura de números. Es importante aclarar que este tipo de actividades no tiene como objetivo que los alumnos dominen la lectura y la escritura de números en otros sistemas, sino que, a partir del contraste, puedan comprender mejor las características y propiedades del sistema decimal posicional.
Se busca además que los niños sean capaces de utilizar la información contenida en la escritura decimal para desarrollar métodos de cálculo exacto o aproximado. Es importante que el docente explicite a los niños que es posible utilizar esa información para resolver cálculos pues no necesariamente todos los alumnos establecen ese vínculo por sí solos.
Intervenciones de enseñanza
A continuación, se retoman las intervenciones propuestas en el documento Progresiones de los aprendizajes. Primer ciclo. Matemática para el trabajo con sistema de numeración, dado que pueden resultar también pertinentes con niños del segundo ciclo ajustándolas en función de los nuevos rangos numéricos:
- Discutir con los alumnos la forma de componer y descomponer cantidades en el trabajo en el contexto del dinero. Es posible plantear juegos donde se usen billetes y monedas de $1, $10, $100, $1.000 y $10.000, etcétera (según el campo numérico que se esté trabajando). Por ejemplo, se puede preguntar: ¿Alcanza con solo mirar el número para saber qué cantidad de billetes de $10, de $100 y de $1.000 y monedas de $1 hay que utilizar para pagar $3.560?
- Generar conclusiones a partir de ese intercambio. Por ejemplo: Si el número tiene cinco cifras, la primera te dice cuántos de diez mil hay, la segunda cuántos de mil, la tercera cuántos de cien, etc.
- Proponer el mismo tipo de trabajo –componer y descomponer números apoyándose en las potencias de 10– en otros contextos. Por ejemplo, a partir de juegos de puntería, o calculadora, etcétera: En el visor de la calculadora aparece el número 25.816, con un solo cálculo convertirlo en 25.016.
- Promover el vínculo entre los distintos contextos en los que se ha trabajado. Por ejemplo: ¿Podemos usar lo que aprendimos con los billetes para averiguar los puntos que se obtienen en los juegos de emboque? Lo que aprendimos con los billetes, ¿sirve para resolver el problema con la calculadora?
En el segundo ciclo es necesario promover, como se señaló, la profundización en el análisis del valor posicional en cuanto a las relaciones entre las distintas posiciones de las cifras en un número: 10 de 10 forman uno de 100; luego también 10 de 100 uno de 1.000, 10 de 1.000 forman 10.000, etcétera, primero entre posiciones contiguas (decenas con centenas; centenas con unidades de mil, etcétera) y luego entre posiciones no contiguas (decenas con unidades de mil, etcétera). Si frente a la situación de tener que determinar cuántos billetes de 100 y monedas de 1 se necesitan para obtener $3.436, un niño no encuentra una estrategia de resolución, es posible preguntarle si se puede armar $1.000 con billetes de $100 (en el caso de que haya en el aula conclusiones escritas sobre esa relación, será valioso remitirlo a ellas). A partir de allí avanzar preguntando: Si con 10 de 100 tengo 1.000, ¿cuánto tendré con 20 billetes de $100?, ¿y con 30? Escribir junto con él esas relaciones que van surgiendo permite sistematizar cierta regularidad (10 de 100 “hacen” 1.000; 20 “hacen” 2.000; etcétera) y dejar esa información disponible para poder recurrir a ella en otras situaciones.
Vincular la recursividad de agrupamientos de a 10 con la multiplicación por 10, 100 y 1.000 permite poner en primer plano el aspecto multiplicativo del sistema de numeración. Por ejemplo:

Es necesario tener en cuenta que cuanto mayor sea el grado de generalidad que se solicite en las formulaciones, la complejidad se incrementa para los niños. Por eso es necesario abordar este contenido en instancias de trabajo colectivo antes de exigir individualmente la disponibilidad de estas conclusiones. Será necesario un progresivo trabajo de contextualizaciones y descontextualizaciones para ir hacia formulaciones más generales.
Hay otras situaciones que permiten avanzar sobre el conocimiento del valor posicional de las cifras. Por ejemplo, problemas del tipo: ¿Cuántos paquetes de 100 ganchitos se pueden armar con 432? ¿Sobran algunos? ¿Cuántos? En este caso, es posible que muchos niños planteen algunos cálculos de división o de multiplicación. Lo central será discutir si es posible responder esa pregunta analizando la información que provee la escritura del número 432 sin necesidad de resolver ningún cálculo. Así la división 432 : 100 podrá ser respondida a partir de utilizar la información que dan las cifras del número. Incorporar este tipo de problemas permite avanzar en otro contexto para profundizar el análisis de las propiedades del sistema de numeración y su relación con la división por la unidad seguida de cero: Si las cifras representan agrupamientos de 10, 100, 1.000, etcétera, será posible, entonces, usar esa información para responder preguntas sobre ese tipo de agrupamientos. En este caso en particular, si en el 432 hay 4 de 100, entonces será posible concluir que se pueden armar 4 paquetes y van a sobrar 32, que no llegan a armar paquetes de 100. Se trata, en definitiva, de hacer confluir la división por 10, 100, 1.000, etcétera y las propiedades de nuestro sistema de numeración. En las discusiones será importante que se haga explícita esa relación. Así, el avance tendrá que ver luego con la posibilidad de descontextualizar esas relaciones, respondiendo estas preguntas: ¿Y cómo podemos saber cuánto da el cociente y el resto de cualquier número dividido 10, 100 o 1.000, sin hacer la cuenta? ¿Es posible? ¿Cómo? Esas formulaciones generales surgidas también pueden volcarse en carteles o textos para las carpetas.
El trabajo con otros sistemas de numeración antiguos, posicionales y no posicionales (la numeración romana, egipcia, china, etcétera) es también una oportunidad para reflexionar sobre las propiedades de nuestro sistema de escritura de números. Es importante aclarar que este tipo de actividades no tiene como objetivo que los alumnos dominen la lectura y la escritura de números en otros sistemas, sino que, a partir del contraste, puedan comprender mejor las características y propiedades del sistema decimal posicional.
Documentos curriculares para consultar
- GCABA, Ministerio de Educación (2017) Matemática. 2º ciclo. Primera parte. Material para el alumno. Aceleración y Nivelación. Serie Trayectorias Escolares. Consultar »
- Gobierno de la Provincia de Buenos Aires, Dirección General de Cultura y Educación, Subsecretaría de Educación, Dirección Provincial de Educación Primaria, Dirección de Gestión Curricular (2007). Matemática Nº 2 A. Numeración. Propuestas para alumnos de 3° y 4° año. Material para el docente. Serie Curricular. La Plata. Consultar »
- Ministerio de Educación de la Ciudad Autónoma de Buenos Aires (2014) Grado de Aceleración 6° / 7°. Matemática. Primer tomo. Números y operaciones, parte 1. Material para el docente. Proyecto Conformación de Grados de Aceleración, pp. 17-31. Consultar »
- Ministerio de Educación de la Ciudad Autónoma de Buenos Aires, DGPLEDU, DCyE (2010) Matemática. Cálculo mental con números naturales. Aportes para la enseñanza. Escuela Primaria, pp. 48-61. Consultar »
- Ministerio de Educación de la Nación (2012) Fascículos Y los números… ¿dónde están?, ¿Hay un lugar para los números? y Cifras a medida. Serie Piedra Libre para todos. Consultar »
- Ministerio de Educación, Ciencia y Tecnología de la Nación (2007) NAP. Matemática 4 y 5. Segundo ciclo EGB / Nivel Primario. Serie Cuadernos para el aula. 4º grado: pp. 38-49 y 5º grado: pp. 38-48. Consultar »