Avanzar en las estrategias de cálculo para resolver problemas de multiplicación y división
Intervenciones de enseñanza
Como se señala en el documento Progresiones de los aprendizajes. Primer ciclo. Matemática, también en el segundo ciclo hay momentos en la enseñanza de la multiplicación y división en los que lo importante es que los niños exploren y reconozcan que es posible usar diversas formas para resolver un mismo cálculo. Más adelante, será necesario que avancen en el tipo de estrategia utilizada, asegurando su dominio. Las estrategias de cálculo utilizadas se relacionan siempre con el tipo de problema que se está resolviendo y/o el tamaño y el tipo de números involucrados. Por ejemplo, es probable que un niño utilice un cálculo multiplicativo para resolver problemas de proporcionalidad, pero necesite realizar esquemas o diagramas en el caso de un problema de combinatoria. También es importante destacar que hay un componente personal en esa elección, hay niños que en distintos momentos se sienten más cómodos o seguros con una u otra estrategia.
Con la intención de promover avances en las estrategias, es posible analizar grupalmente o con algún niño en particular la relación entre diferentes procedimientos para resolver un mismo cálculo, las similitudes que tienen entre ellos y la economía que permiten. También, relacionar los procedimientos con las propiedades de las operaciones da lugar a que los niños adviertan cuáles se están utilizando, y puedan identificarlas y nombrarlas. A partir de este trabajo, el docente puede proponer situaciones que exijan la utilización de las propiedades de las operaciones para argumentar acerca de la validez o no de un procedimiento.
Nuevamente cabe advertir que no es esperable que todos los niños avancen al mismo tiempo en la construcción de estrategias ni se espera que prevalezca una única manera de resolver. Tampoco es esperable que cada niño tenga necesariamente que “inventar” los distintos procedimientos. Por eso, cuando en el aula aparece una idea potente o el maestro decide presentar un procedimiento relevante, es importante promover que todos los chicos tengan la posibilidad de ensayar esa idea y poner en juego ese procedimiento.
Para que los niños avancen en sus estrategias de cálculo es importante:
- Continuar el trabajo de memorización de un repertorio de cálculos simples de multiplicación,
iniciado en primer ciclo. Tener disponibles en la memoria los resultados
de algunos cálculos se puede convertir en un apoyo para resolver otros cálculos más
complejos. Para lograrlo es importante que los niños puedan reconocer por sí mismos
cuáles son aquellos cálculos “en los que nunca se equivocan”. Se puede proponer hacer
un listado de tablas fáciles o de resultados que ya saben de memoria, o que distingan,
dentro de un conjunto de productos, para cuáles conocen el resultado y para cuáles no.
Este tipo de actividades favorece la toma de conciencia de lo que se ha aprendido y la identificación de que hay algo sobre lo que es necesario continuar trabajando. - Retomar el análisis y la sistematización de multiplicaciones por 10, 100 y 1.000, etcétera, y por otros números “redondos” (por 20, 30, 200, etcétera), estudiadas en primer ciclo. Esto es importante para que luego se puedan discutir y generalizar procedimientos de multiplicación de números mayores.
- Proponer el uso de cálculos simples para resolver otros más complejos. Por ejemplo, para resolver 26 × 12 se puede analizar si es posible apoyarse en 26 × 10 que es un resultado fácil de obtener, o en 26 × 6 que implica multiplicar por una sola cifra, y discutir entonces qué habría que hacer para llegar al resultado a partir de ellos. Luego de ese trabajo se pueden escribir esas conclusiones en un cartel referido a un caso particular discutido, que sirva luego para otros casos similares. El siguiente es un ejemplo posible.
- Promover la difusión de diversos procedimientos de cálculo. Hay momentos en los procesos de enseñanza en que lo importante es la exploración y el reconocimiento de diversas formas de resolver un mismo cálculo. El registro siguiente muestra distintos modos de resolver 15 × 14.
- Promover el análisis de las propiedades aritméticas que subyacen a una cierta estrategia de cálculo utilizada. En los procedimientos del ejemplo anterior se pone en juego la propiedad distributiva de la multiplicación. Explicitarla o no dependerá del momento y del propósito de enseñanza.
- Presentar el algoritmo por dos cifras luego de haber desplegado y analizado en la clase diversas opciones de cálculo para resolver multiplicaciones de números mayores. La presentación del algoritmo tiene que estar apoyada y ser consecuencia de ese trabajo de descomposiciones en las que se relacionan sumas y multiplicaciones. Hay algunas formas de representación que pueden ayudar a explicitar cuáles son los cálculos intermedios ocultos en el algoritmo de la multiplicación. El trabajo con problemas de organizaciones rectangulares puede funcionar en ese sentido. Por ejemplo, frente al problema: En el teatro hay 24 filas de 16 butacas cada una, ¿cuántos espectadores entran en el teatro cuando está lleno?, es una estrategia pertinente mostrar en los gráficos que representan la situación las multiplicaciones parciales en juego, vinculando esta representación con los cálculos intermedios del algoritmo.
- Promover el trabajo con situaciones de cálculo aproximado para que se constituya progresivamente en una herramienta de anticipación y control de los cálculos que se realizan. En este sentido se puede proponer a los niños la resolución de situaciones como la siguiente:
| Lucía | 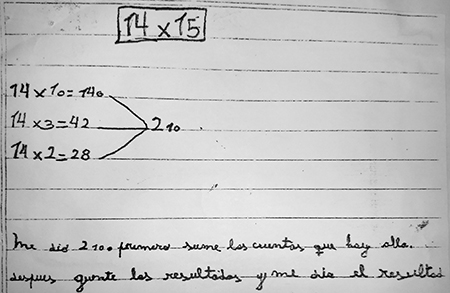 |
| Sebastían |  |
| Brisa | 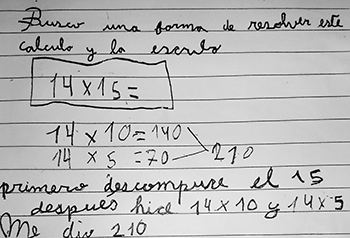 |
| José |  |
No se trata solamente de socializar estas opciones diversas, sino que lo valioso es además analizar grupalmente (y retomarlo luego con algún niño en particular si es necesario) la relación que hay entre estos diferentes procedimientos para resolver un mismo cálculo. Detenerse sobre los procedimientos contribuye a que los alumnos adopten una posición reflexiva sobre su trabajo matemático. Establecer vínculos entre procedimientos diferentes –exitosos o no– probablemente dé lugar a nuevas relaciones que no necesariamente estuvieron en juego en la resolución de cada alumno y que son claramente producto de la interacción. Por un lado, es posible considerar las diferencias que tienen. En este caso, se podría analizar que en algunos procedimientos se descompone el 14 y en otros el 15 de diversas maneras (el 14 como 10 + 4 y el 15 como 10 + 5 o 10 + 3 + 2) para que los niños adviertan que en todos ellos el 15 se repite 14 veces o el 14, 15 veces. También, por otro lado, es valioso analizar las similitudes y la economía que alguno de ellos permite. En este caso, se pueden comparar los dos últimos procedimientos ya que se apoyan en descomposiciones similares, pero en uno se multiplica y en otro se suma. Al poner en relación dos procedimientos los niños se ven confrontados a encontrar en uno de ellos relaciones que están más claramente explicitadas en el otro. En el caso de nuestro ejemplo, se podría preguntar: Este cálculo de 14 × 10 que hizo Brisa, ¿está de alguna manera en el cálculo de José? ¿Dónde? Acá hay una suma y acá una multiplicación, ¿habrá alguna manera de convertir esta suma en una multiplicación? ¿El 10 que está en esta suma significa lo mismo que el 10 que está en esta multiplicación? Estas preguntas buscan provocar comentarios de los niños que el docente puede retomar y completar para explicar la relación entre los procedimientos.
También es valioso proponer el análisis de los errores que se pueden producir en los procedimientos de cálculo mental. Cuando los alumnos ensayan descomposiciones para poder multiplicar números mayores suelen cometer errores relacionados con descomposiciones incompletas o fruto de no realizar todas las multiplicaciones necesarias si la descomposición afecta a ambos factores. A continuación, se propone un ejemplo.

En este caso, el alumno descompuso ambos factores (el 14 como 10 + 4 y el 15 como 10 + 5) pero no fue exhaustivo al realizar las multiplicaciones necesarias: multiplica 10 × 10 y 5 × 4, pero no considera multiplicar 10 × 4 y 10 × 5. Se podría hipotetizar que, apoyado en descomposiciones y procedimientos habituales a la hora de sumar –en los que se puede sumar unidades con unidades y decenas con decenas–, extiende esta opción a la hora de realizar la multiplicación. Frente a una situación como esta es importante confrontar esta opción con otras que hayan surgido y reconocer en qué casos se está “haciendo 14 veces el 15”.
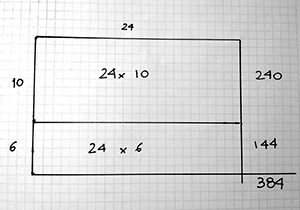
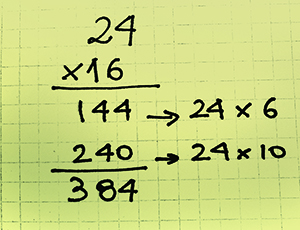
Por supuesto, este modo de representar los problemas de organizaciones rectangulares tiene que haber sido objeto de trabajo anterior, incluso con números menores. Por otra parte, acudir a este tipo de representación resulta, en general –y no solamente para problemas de organizaciones rectangulares–, una herramienta potente para facilitar la comprensión de las descomposiciones implicadas en las estrategias de cálculo de multiplicación.
Un error habitual en el algoritmo de la multiplicación es que los niños encolumnen mal los números a sumar sin considerar el valor posicional de las cifras. Por ejemplo:
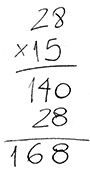
Volver a las descomposiciones que están detrás del procedimiento algorítmico, analizando que el 15 se descompone en la suma 10 + 5 es necesario para que los alumnos puedan considerar aquello que está oculto. Registrar en un cartel los cálculos intermedios involucrados puede ser útil para volver cuando sea necesario. Por ejemplo:
| En la cuenta de multiplicar, se desarma uno de los números (factores) y se multiplica primero por las unidades y luego por los dieces (decenas) que lo forman. Luego se suman ambos resultados. En el ejemplo, el 15 fue desarmado como un 10 y un 5. |
Escribir el cero en el lugar de las unidades (en el 280) permite hacer evidente que se está multiplicando allí por 10 y no por 1.
| 1. Marcá el resultado correcto sin hacer la cuenta. | |||
| 375 × 23 = 2.581 × 19 = |
6.625 49.039 |
8.625 28.039 |
10.625 61.039 |
| 2. Encuadrá el resultado de cada cuenta. ¿Cómo lo pensaste? | |||
| 5 × 22 49 × 51 |
entre 100 y 1.000 entre 100 y 2.000 |
entre 1.000 y 10.000 entre 2.000 y 3.000 |
entre 10 y 100 entre 3.000 y 4.000 |
Uno de los objetivos del segundo ciclo es que los niños avancen en sus estrategias de resolución
de cálculos de división. Es importante subrayar que el algoritmo de la división
no es el único procedimiento posible para realizar los cálculos. Por otro lado, aprender
a dividir es mucho más que conocer el algoritmo, más aun teniendo en cuenta que hoy
están ampliamente disponibles instrumentos como la calculadora que permiten realizar
esos cálculos. Saber dividir es reconocer cuáles son los problemas en los que se puede usar
una división para resolverlos y cuáles no; es entender las relaciones que se establecen entre
el dividendo, el divisor, el cociente y el resto; es decidir si el resto tiene o no un papel en
la respuesta a un problema y es también disponer de diversos procedimientos de cálculo.
A continuación, se proponen algunas sugerencias para la intervención en el aula:
A continuación, se proponen algunas sugerencias para la intervención en el aula:
- Es importante hacer explícita la relación entre multiplicación y división. En ese sentido es central retomar el trabajo iniciado en 3º grado estableciendo que 32 ∶ 8 es igual a averiguar por cuánto hay que multiplicar a 8 para obtener 32, y el uso de la tabla pitagórica es una herramienta que permite encontrar el resultado de una división (y no solo de una multiplicación). Se pueden prever propuestas que avancen en un primer momento en la relación de la multiplicación con la división sobre números que están en la tabla pitagórica (por ejemplo 42 ∶ 7); luego con divisiones con resto diferente de 0 pero que encuentran respuesta en la tabla (por ejemplo 39 ∶ 5). En estos casos, es importante discutir con los alumnos que, si bien el número a dividir no se encuentra directamente en la tabla, es posible utilizarla ubicando otro número cercano pertinente. Es valiosa la discusión sobre cuál es el número de la tabla que sirve, ya que a veces los niños eligen el número que está más cercano al dividendo, sin considerar que debe ser menor que él y no mayor. Intervenir, recuperando la relación de los números con el problema que se está resolviendo puede resultar fértil. Por ejemplo: ¿Podés usar 40 caramelos para repartir si solo tenés 39? Si le das 8 a cada uno, usás 40 caramelos, ¿tenés 40 caramelos para usar? ¿Cuántos caramelos dice el problema que teníamos?, etcétera. Finalmente, se trata de avanzar con cálculos que se extiendan a números mayores que ya no están presentes en la tabla (por ejemplo 84 ∶ 7), para que por último los niños empiecen a aproximar el cálculo mental usando las multiplicaciones por 10, 100, 1.000, por 20, 30, etcétera. Por supuesto, para que esta relación entre la multiplicación y la división pueda construirse con sentido, es necesario que antes los niños hayan tenido la oportunidad de resolver muchos y variados problemas de repartos y particiones, ensayando diversos procedimientos a través de gráficos, cálculos de suma o resta. Este es un trabajo fuerte de primer ciclo que hay que retomar al inicio de segundo ciclo.
- La presentación de los algoritmos tiene que estar precedida de un fuerte trabajo sobre estrategias diversas de cálculo mental. El algoritmo introduce una forma diferente de organizar los procedimientos y las escrituras que efectivamente ya se realizan. Una vez que la mayor parte de los niños resuelve divisiones mediante aproximaciones multiplicativas, se podría presentar el algoritmo extendido de la división, relacionándolo con esos procedimientos.
- En muchos casos, puede ser una ayuda registrar las multiplicaciones intervinientes y relacionar gráficamente esas multiplicaciones con sus resultados. Escribir todas las multiplicaciones que se van utilizando también es un apoyo útil para poder controlar y reconstruir los pasos que se fueron haciendo cuando se hace necesario revisar el procedimiento frente a un error. La transparencia de los cálculos intermedios que se realizan ayuda a la comprensión y al control.
- Cuando se proponen situaciones para que los niños resuelvan divisiones con números mayores es muy importante que los divisores elegidos sean números que permitan cálculos de multiplicación más o menos sencillos (24, 15, 32, etcétera). No tiene sentido en la enseñanza presentar divisiones de números muy grandes, con divisores que resulten complejos de “manipular”.
- Un avance posterior será lograr que los niños “acorten” los pasos intermedios involucrados en el procedimiento algorítmico. A continuación, se analiza un ejemplo posible de intervención que permitiría el avance en ese sentido.
- Presentar un cálculo ya resuelto y proponer que se vuelva a realizar, pero en menor cantidad de pasos.
- Proponer realizar una cuenta a partir de algunas multiplicaciones ya dadas, para que se pueda elegir las más convenientes.
- Enseñar a realizar cálculos estimativos resulta fundamental para que los alumnos construyan estrategias de anticipación y control de los resultados obtenidos, tanto cuando realizan cálculos mentales, algorítmicos o cuando utilizan la calculadora. Saber con anticipación entre qué números puede estar el resultado de un cálculo es un conocimiento que luego permite controlar si el resultado obtenido es posible o no. Es interesante cuando se enseña a los niños a estimar el resultado de un cálculo pedirles por un tiempo que primero hagan la estimación, luego el cálculo y al final controlen con la calculadora el resultado obtenido. En el caso de la división, la estimación de los resultados está ligada a las multiplicaciones por potencias de 10.
- Una de las razones por las cuales el cálculo de división entera resulta más complejo que otros cálculos tiene que ver con que, como resultado del procedimiento, se obtienen dos números: el cociente y el resto. Esto solo sucede en el caso de esta operación. Es importante abordar desde la enseñanza la relación entre estos dos resultados y el problema que se busca resolver, así como la relación entre las distintas partes que conforman el cálculo (el dividendo, el divisor, el cociente y el resto). A partir de instancias colectivas de discusión se podría armar, por ejemplo, un cartel como el siguiente:
Las siguientes son producciones de niños que se apoyan en cálculos multiplicativos (multiplicaciones por 10, o por 10, 11, 12, etcétera) para resolver situaciones de división.


En otra situación, frente al problema Manuel tiene que repartir 90 huevos en hueveras de 6 cada una. ¿Cuántas hueveras puede llenar?, otro alumno resuelve de esta manera:
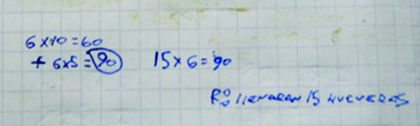
A partir del análisis de estos procedimientos, en particular de los procedimientos similares al último, se podrían escribir conclusiones que sistematicen las estrategias que se apoyan en aproximaciones multiplicativas. Un ejemplo podría ser:
|
Cuando dividimos números que no están en la tabla pitagórica pues son números más grandes que los
que están en ella, podemos ir repartiendo por partes hasta completar un total.
Por ejemplo, para dividir 80 caramelos en bolsas de a 5 caramelos, podemos pensar que 10 × 5 = 50, entonces puedo armar 10 bolsas, usando 50 caramelos, y quedan 30 caramelos por embolsar. Con esos 30 puedo armar 6 bolsas pues 6 × 5 = 30. Entonces, finalmente armamos primero 10 bolsas, luego 6 bolsas, son 16 bolsas en total. |
Estos pasos de resolución que realizan los niños son muy similares al funcionamiento que tiene el algoritmo de la división.
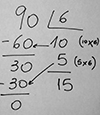
Puede resultar valioso, y ayuda a dar sentido a ese procedimiento, que se vincule cada paso del cálculo con el problema que se está resolviendo. En este: Uso 10 hueveras, entonces saco 60 huevos (6 × 10) y los resto a los 90. Todavía me quedan 30 huevos por ubicar (90 – 60). Puedo usar 5 hueveras en las que entran 30 huevos (5 × 6), etcétera. Lo que está detrás de este procedimiento es la posibilidad de hacer repartos “por partes” apoyándose en las multiplicaciones por 10, por 100 o por otros números redondos.
Joaquín produjo este cálculo:
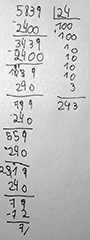
Frente a esta producción, el docente podría preguntar: Acá pusiste dos veces el 100, ¿podría ponerse directamente el 200? Entonces, ¿cuánto tendrías que restar? ¿Podría ser?, con la intención de que el alumno pueda empezar a reconocer que multiplicar dos veces por 100 es como multiplicar por 200 directamente. Lo mismo para el uso del 10 reiteradas veces. Esto requiere que se haya trabajado previamente la multiplicación por números múltiplos de 10 (20, 30, 40, 200, 300, etc.).
Hay varias actividades posibles que tienen como propósito ayudar a los niños a “acortar” los pasos intermedios y hacer más eficiente este procedimiento. A continuación, se describen algunos ejemplos, entre otros posibles, de estas actividades:
|
Acortá esta cuenta para que quede resuelta en menos pasos.
|
|
Resolvé la siguiente división usando las multiplicaciones que te sirvan.
|
Como ya se señaló, es importante recordar que el algoritmo no debe ser la cuestión central de trabajo en la enseñanza de la división. El esfuerzo tiene que estar puesto en que los alumnos puedan reconocer cuándo la división es un cálculo apropiado para utilizar en la resolución de una situación. Por eso, en muchas situaciones es conveniente proponer a los niños que usen la calculadora para encontrar la respuesta a los cálculos en lugar de resolver “con lápiz y papel”.
Por ejemplo, antes de realizar el cálculo 5.950 ∶ 28, se puede proponer a los niños realizar algo similar a lo siguiente:
|
El resultado… ¿Podrá ser 10?; 28 × 10 = 280, es muy poco. ¿Podrá ser 100?; 28 × 100 = 2.800, es muy poco. ¿Podrá ser 1.000?; 28 × 1.000 = 28.000, me pasé. Entonces el resultado tiene que ser más de 100 y menos de 1.000. |
A partir de esta discusión, se podrá establecer con los niños que el cociente tendrá entonces tres cifras. En este sentido un avance esperable es que los niños puedan realizar estimaciones más precisas. Siguiendo el mismo ejemplo, se podría preguntar si el resultado dará más o menos de 500, o si va a estar más cerca de 100 o de 1.000.
Algunos ejemplos de actividades para trabajar la estimación de resultados en cálculos de división:
|
Sabiendo que: 24 × 10 = 240 24 × 100 = 2.400 24 × 1.000 = 24.000 24 × 10.000 = 240.000 Indicá si: a) 245 ∶ 24 va a dar un número mayor, menor o igual a 10 b) 2.000 ∶ 24 va a dar un número mayor, menor o igual a 100 c) 23.598 ∶ 24 va a dar un número mayor, menor o igual a 1.000 d) 32.597 ∶ 24 va a dar un número mayor, menor o igual a 1.000 |
| Para cada una de las siguientes divisiones, te proponemos tres números. Señalá el más cercano al cociente y explicá cómo te diste cuenta. | |||
| a) 436 ∶ 25 | 20 | 10 | 30 |
| b) 6.000 ∶ 45 | 100 | 200 | 300 |
| c) 738 ∶ 95 | 10 | 15 | 5 |
Encuadrar el cociente entre dos potencias de 10 es una estrategia que puede resultar de ayuda tanto para controlar el resultado de una división como para anticipar, antes de realizar el cálculo, la cantidad de cifras del cociente.
Completá la siguiente tabla de resultados aproximados de la división. El resultado de cada cálculo será:
|

Documentos curriculares para consultar
- GCABA, Ministerio de Educación (2014) Grado de Aceleración 4° / 5°. Matemática. 2° y 3° Bimestre. Material para el docente. Consultar »
- GCABA, Ministerio de Educación (2014) Grado de Aceleración 6° / 7°. Matemática. 1° Bimestre. Material para el docente. Consultar »
- GCABA, Ministerio de Educación (2017) Matemática. Segundo ciclo. Segunda parte. Aceleración y Nivelación. Serie Trayectorias Escolares. Consultar »
- GCABA, Ministerio de Educación, DGPLEDU, Dirección de Currícula y Enseñanza (2010) Matemática. Cálculo mental con números naturales. Aportes para la enseñanza. Escuela Primaria, pp. 37-56. Consultar »
- GCABA, Secretaría de Educación, Dirección General de Planeamiento, Dirección de Currícula (2001) Actualización Curricular. 7º grado. Documento de trabajo. Consultar »
- Gobierno de la Provincia de Buenos Aires, Dirección General de Cultura y Educación, Subsecretaría de Educación, Dirección Provincial de Educación Primaria, Dirección de Gestión Curricular (2007) Matemática Nº 3 A. Operaciones con números naturales 1ª parte. Propuestas para alumnos de 3º y 4º año. Material para el docente. Serie Curricular. La Plata Consultar »
- Gobierno de la Provincia de Buenos Aires, Dirección General de Cultura y Educación, Subsecretaría de Educación, Dirección Provincial de Educación Primaria, Dirección de Gestión Curricular (2007) Matemática N° 5 A. Operaciones con números naturales. 2ª parte. Propuestas para alumnos de 3° y 4° año. Material para el docente. Serie Curricular. La Plata. Con propuestas de cálculo mental. Consultar »
- Gobierno de la Provincia de Buenos Aires, Dirección General de Cultura y Educación, Subsecretaría de Educación, Dirección Provincial de Educación Primaria, Dirección de Gestión Curricular (2007) Juegos que pueden colaborar en el trabajo en torno al cálculo mental. Área Matemática. Material para el docente. Mejorar los aprendizajes. Versión preliminar. La Plata. Consultar »
- Gobierno de la Provincia de Buenos Aires, Dirección General de Cultura y Educación, Subsecretaría de Educación, Dirección Provincial de Planeamiento, Dirección de Producción de Contenidos (2007) División en 5º y 6º año de la escuela primaria. Una propuesta para el estudio de las relaciones entre dividendo, divisor, cociente y resto. Documento de apoyo para la capacitación. Consultar »
- Ministerio de Educación de la Nación (2012) Cuadernillo Múltiples problemas. Serie Piedra Libre. Consultar »
- Ministerio de Educación de la Nación (2012) Matemática para todos en el Nivel Primario. Notas para la enseñanza. Vol. 1. Operaciones con números naturales, pp. 9-25 y 41-55. Consultar »
- Ministerio de Educación de la Nación. Matemática. Para seguir aprendiendo. Tareas de acompañamiento para alumnos y alumnas de 4º y 5º grado. Cuadernillo de actividades. Serie Aprender con todos. Consultar »
- Ministerio de Educación, Ciencia y Tecnología de la Nación (2007) NAP. Matemática 4 y 5. Segundo ciclo EGB / Nivel Primario. Serie Cuadernos para el aula. 4º grado: pp. 79-105 y 5º grado: pp. 68-84. Consultar »