Comprender problemas
En el segundo ciclo, el avance en el aprendizaje de las operaciones incluye resolver problemas
que amplíen los sentidos de las operaciones trabajados en primer ciclo. De esta
forma se introducen nuevos tipos de problemas en los que resulta menos evidente para
los niños la relación entre las situaciones planteadas y las operaciones de multiplicación y
división (por ejemplo, problemas de combinatoria, problemas de división en los que no
hay repartos, entre otros).
En el primer contacto con un nuevo tipo de problemas es deseable favorecer que los alumnos puedan desplegar procedimientos diversos que les permitan encontrar la respuesta. Es probable que frente a una situación de reparto como: Hay que distribuir 5.600 libros en cajas de 35 libros, ¿cuántas cajas se necesitan para colocarlos a todos?, algunos alumnos reconozcan que es posible usar la división. Sin embargo, frente a esta otra situación: Ana María tiene en el banco $16.650. Todos los días retira $370. ¿En cuántos días habrá retirado todo el dinero?, es probable que esos mismos alumnos no reconozcan directamente que allí también es posible realizar una división y apelen a otros procedimientos como sumas o restas sucesivas, aproximaciones mediante multiplicaciones parciales, etcétera. Resulta conveniente explicitar a los alumnos que pueden recurrir a diferentes estrategias: dibujos, esquemas, cuentas según lo que necesiten, con el fin de habilitar en el aula el permiso a probar diversas formas de resolver.
También es posible que algunos niños, frente a un problema de un nuevo tipo, digan que no entienden cómo resolverlo o que lo resuelvan incorrectamente. Un paso importante para destrabar la situación es que logren hacerse una representación de la situación que plantea el problema. El maestro puede ayudar a que eso suceda. Para proporcionar esta ayuda necesitará identificar aquello que en la formulación del enunciado podría constituir un obstáculo: una situación que no es familiar, terminología que no es conocida, etc.
Algunas intervenciones posibles son:
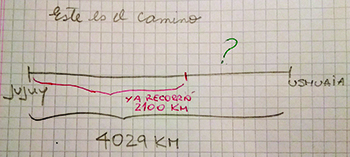
Por ejemplo, para el problema: Joaquín está haciendo un viaje desde San Salvador de Jujuy hasta Ushuaia. La distancia total es de 4.029 kilómetros. Si ya recorrió 2.100 kilómetros, ¿cuántos kilómetros le falta recorrer?, se podría armar con los niños una representación como la que se incluye debajo, porque graficar la situación puede ayudar a comprender lo que se pregunta y a elaborar una estrategia posible: se trata de averiguar la distancia entre 2.100 y 4.029, ¿cuánto le falta a 2.100 para llegar a 4.029? De esta manera discutir entonces qué operación matemática sirve para esa búsqueda: completar una suma 2.100 + …… = 4.029 (suma que se puede completar apoyándose en repertorios trabajados), o bien, realizar una resta.
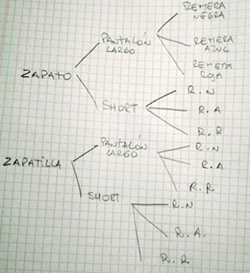
Las representaciones en esquemas o diagramas son herramientas de las que los niños se deben ir apropiando progresivamente. Contribuyen a identificar y establecer semejanzas entre problemas. En ese sentido, los diagramas de árbol merecen una mención especial. Son particularmente pertinentes en el caso de los problemas de combinatoria dado que permiten encontrar un modo de contar exhaustivamente las combinaciones posibles entre elementos de los conjuntos involucrados. El siguiente es un ejemplo de resolución –utilizando un diagrama– de un problema de combinatoria en el que se pide averiguar todas las combinaciones posibles entre remeras (negra, azul y roja), pantalones (largos o shorts) y calzado (zapatillas o zapatos).
Así, en nuevos problemas, decidir si es posible o no utilizar un diagrama similar al ya utilizado en otros anteriores puede contribuir a su mejor comprensión y a encontrar entonces más fácilmente una estrategia de resolución. Puede resultar valioso que luego, en situaciones colectivas de discusión, se establezcan vínculos entre estos procedimientos con el cálculo de la multiplicación.
Después de la instancia de resolución es importante dar lugar a la reflexión sobre lo trabajado. La socialización de procedimientos posibles, que hayan surgido en el grupo o que el maestro considere pertinente aportar, permite que circulen entre los alumnos estrategias diversas. Algunas cuestiones importantes a considerar en ese sentido son:
Frente a soluciones erróneas, por ejemplo porque el niño elige una operación incorrecta o porque usa todos los números del enunciado (aun los que no son pertinentes), se puede:
Otras sugerencias posibles para el trabajo en el aula con problemas son:
El caso de los problemas de proporcionalidad
En el segundo ciclo ocupa un lugar central el trabajo con problemas de proporcionalidad. Al plantear su enseñanza, es necesario tener en cuenta que la proporcionalidad se inscribe en el campo de lo multiplicativo, e implica un conjunto de conceptos relacionados, que se adquieren simultáneamente durante un período prolongado de tiempo. El aprendizaje de este contenido, como sucede también con otros centrales del ciclo, no termina en la escuela primaria. En la escuela secundaria será retomado y resignificado.
A lo largo del ciclo se pueden plantear problemas de diversa complejidad. Esa variación en la complejidad está dada, entre otras cuestiones, por:
A partir del trabajo con situaciones de proporcionalidad se espera que, por un lado, los niños puedan identificar cuál es el tipo de vínculo que hay entre las magnitudes que se relacionan proporcionalmente y por lo tanto puedan reconocer cuándo dos magnitudes son proporcionales o no; y por otro lado, que puedan entonces, en situaciones de proporcionalidad, encontrar nuevos valores a partir de otros dados, poniendo en juego la constante de proporcionalidad o las propiedades que caracterizan a esa relación:
Algunas consideraciones para tener en cuenta:
En el primer contacto con un nuevo tipo de problemas es deseable favorecer que los alumnos puedan desplegar procedimientos diversos que les permitan encontrar la respuesta. Es probable que frente a una situación de reparto como: Hay que distribuir 5.600 libros en cajas de 35 libros, ¿cuántas cajas se necesitan para colocarlos a todos?, algunos alumnos reconozcan que es posible usar la división. Sin embargo, frente a esta otra situación: Ana María tiene en el banco $16.650. Todos los días retira $370. ¿En cuántos días habrá retirado todo el dinero?, es probable que esos mismos alumnos no reconozcan directamente que allí también es posible realizar una división y apelen a otros procedimientos como sumas o restas sucesivas, aproximaciones mediante multiplicaciones parciales, etcétera. Resulta conveniente explicitar a los alumnos que pueden recurrir a diferentes estrategias: dibujos, esquemas, cuentas según lo que necesiten, con el fin de habilitar en el aula el permiso a probar diversas formas de resolver.
También es posible que algunos niños, frente a un problema de un nuevo tipo, digan que no entienden cómo resolverlo o que lo resuelvan incorrectamente. Un paso importante para destrabar la situación es que logren hacerse una representación de la situación que plantea el problema. El maestro puede ayudar a que eso suceda. Para proporcionar esta ayuda necesitará identificar aquello que en la formulación del enunciado podría constituir un obstáculo: una situación que no es familiar, terminología que no es conocida, etc.
Algunas intervenciones posibles son:
- Pedir al niño que reformule lo que sí entendió del enunciado. Se trata de ayudarlo a expresar lo que comprendió, eventualmente iniciando el relato y dándole lugar a continuarlo.
- Releer el problema junto con el alumno.
- Ayudar a identificar la incógnita y los datos que se presentan.
- Modificar los números en juego –por números más pequeños o redondos, por ejemplo–, proponer que resuelva con esos números y luego volver, si es posible, a pensar nuevamente el problema original.
- Remitir a enunciados similares trabajados anteriormente para establecer relaciones con el nuevo problema. Por ejemplo: En el problema de la panadería, que hicimos ayer, tuvimos que repartir panes en los canastos. En este problema de hoy, ¿hay que repartir también? ¿Nos sirve ahora lo que usamos con los panes?
- Leer conclusiones anteriores que se hayan registrado y sean pertinentes para la nueva resolución. Por ejemplo, si a partir del trabajo con problemas de división se ha discutido y escrito en un cartel: En los problemas en los que hay que averiguar cuántas veces entra un número en otro, se puede dividir; se puede leer cuando algún alumno o grupo de alumnos enfrente otras situaciones similares.
- Proponer a los alumnos que dibujen, iniciar un dibujo para que lo continúen o producir junto a los niños esquemas que representen la situación.
Por ejemplo, para el problema: Joaquín está haciendo un viaje desde San Salvador de Jujuy hasta Ushuaia. La distancia total es de 4.029 kilómetros. Si ya recorrió 2.100 kilómetros, ¿cuántos kilómetros le falta recorrer?, se podría armar con los niños una representación como la que se incluye debajo, porque graficar la situación puede ayudar a comprender lo que se pregunta y a elaborar una estrategia posible: se trata de averiguar la distancia entre 2.100 y 4.029, ¿cuánto le falta a 2.100 para llegar a 4.029? De esta manera discutir entonces qué operación matemática sirve para esa búsqueda: completar una suma 2.100 + …… = 4.029 (suma que se puede completar apoyándose en repertorios trabajados), o bien, realizar una resta.

Las representaciones en esquemas o diagramas son herramientas de las que los niños se deben ir apropiando progresivamente. Contribuyen a identificar y establecer semejanzas entre problemas. En ese sentido, los diagramas de árbol merecen una mención especial. Son particularmente pertinentes en el caso de los problemas de combinatoria dado que permiten encontrar un modo de contar exhaustivamente las combinaciones posibles entre elementos de los conjuntos involucrados. El siguiente es un ejemplo de resolución –utilizando un diagrama– de un problema de combinatoria en el que se pide averiguar todas las combinaciones posibles entre remeras (negra, azul y roja), pantalones (largos o shorts) y calzado (zapatillas o zapatos).

Así, en nuevos problemas, decidir si es posible o no utilizar un diagrama similar al ya utilizado en otros anteriores puede contribuir a su mejor comprensión y a encontrar entonces más fácilmente una estrategia de resolución. Puede resultar valioso que luego, en situaciones colectivas de discusión, se establezcan vínculos entre estos procedimientos con el cálculo de la multiplicación.
Después de la instancia de resolución es importante dar lugar a la reflexión sobre lo trabajado. La socialización de procedimientos posibles, que hayan surgido en el grupo o que el maestro considere pertinente aportar, permite que circulen entre los alumnos estrategias diversas. Algunas cuestiones importantes a considerar en ese sentido son:
- Decidir qué procedimientos elegir para poner en discusión dependerá de los propósitos de enseñanza y las posibilidades que el conjunto de alumnos haya movilizado. A veces, es posible que algún niño produzca una estrategia valiosa, pertinente y muy elaborada, pero que puede resultar aún demasiado compleja de comprender para la mayoría los alumnos. No se trata de discutir todas las opciones que surjan en la clase. Por otro lado, es importante que durante esa socialización las preguntas se dirijan a toda la clase y no solo al autor de la resolución que se está analizando: Para resolver 42 × 15, Miguel cuenta que hizo 40 × 15 y 2 × 15, ¿de dónde salió ese 40 que usó Miguel?
- Detener el análisis en momentos parciales de la resolución de un alumno para considerar la relación entre los cálculos realizados y el problema a resolver: ¿Hasta acá qué es lo que averiguamos? ¿Y qué falta averiguar?
- Establecer relaciones entre problemas distintos pero que se resuelven con la misma operación. En segundo ciclo, se amplía el tipo de problemas que se resuelven con la división y la multiplicación. Generar momentos de análisis de las diferencias y similitudes entre problemas y establecer conclusiones sobre eso son situaciones fértiles para establecer la relación entre nuevos problemas y otros anteriores que apelan a distintos sentidos de una misma operación.
- También es posible armar carteles que se refieran particularmente a las conclusiones a propósito del análisis de enunciados de los problemas. Por ejemplo, a partir del trabajo sobre los datos de un enunciado se podría concluir:
- Hay algo que no sabemos y tenemos que averiguar. A veces eso que necesitamos averiguar se señala en forma de pregunta. Las preguntas aparece encerradas con los signos “¿?”.
- En el problema hay información que se usa para averiguar lo que no sabemos. Son los datos que, a veces, se muestran como números. Hay que tener en cuenta que no siempre todos los datos que tiene el problema sirven para resolver lo que se pregunta.
Los siguientes diálogos producidos durante una clase son ejemplos de este tipo de situaciones. En ambos ejemplos el docente interviene para promover vínculos entre un problema que acaban de resolver los alumnos y otros problemas resueltos en clases anteriores. En la primera situación se vinculan problemas de división que implican sentidos distintos. En la segunda situación, se promueve la relación entre problemas de división similares en contextos diferentes.
|
Situación 1
En clases anteriores, los chicos habían estado resolviendo problemas de reparto y partición. En esta clase se enfrentan por primera vez con un problema de división en el que se moviliza un sentido diferente: Joaquín cobró $370; si gasta en comida $12 ¿para cuántos días le alcanza? ¿Cuánta plata le queda para comer al día siguiente? Cuando cada grupo termina de trabajar, se realiza la puesta en común. Maestra: ¿Saben lo que me quedé pensando? […] Leo le dijo a su equipo que no podía ser una división porque no es un problema de repartir. ¿Tiene razón o no? Pedro: Está mal… Cristian O: No, no tiene razón... No se reparte ¿cómo te puedo explicar? No es como que se reparte, es como que… Es un problema de gastar. Maestra: Entonces si es de gastar ¿es un problema de menos, como dijo Leo? David: Cuando es de división te das cuenta porque la pregunta te dice que tenés que repartir. Pedro: Sí, pero este es como que reparte la plata en días… es como que tenés la plata y le das a chicos. David: Es como si los días fueran chicos y hay que darle 12 a cada uno. Maestra: Entonces, yo sé que tengo que darle 12 a cada uno y no sé para cuántos me alcanza. Lo que no sé es cuántos “doces” puedo sacar. ¿Saben lo que dijeron unos chicos de otro grado resolviendo este problema? Varios: No, ¿qué? Maestra: …qué había que ver “cuántos 12 entraban en 370”... David: Sí, es así. Cristian O: Una cuenta de multiplicar 30 veces 12, son 30 los que entra. Maestra: Entonces, es un problema en el que hay que averiguar cuántas veces entra el 12, ¿es correcto decirlo? Cristian O: Si hacés 12, 12, 12, 12, hacés directo 12 × 10 y es 120 y ves que podés más y 12 × 20 es 240 y 12 × 30 te da 360 y entonces parás… Maestra: Entonces, si es un problema en el que hay que armar grupitos de 12… Leo: Armar grupos… Entonces ¡es una división! |
|
Situación 2
En la clase siguiente los chicos resuelven este problema: Si estoy en el número 389 y doy saltos de 6 en 6 para atrás, ¿a qué número llego antes del 0? Luego de la resolución, la maestra destina un momento a la reflexión compartida e interviene para provocar que se establezca una relación entre este nuevo problema y uno similar, pero ubicado en otro contexto, resuelto en la clase anterior. Maestra: Quiero que pensemos juntos en el problema que hicimos el viernes pasado. ¿Se acuerdan de ese problema? Búsquenlo todos en la carpeta. […] ¿En qué se parece ese problema que hicimos con este de “dar saltos para atrás”? Karen: No, porque ese era de comida, este es de saltos. Leo: No, nada que ver…ése era de plata… David: ¡Sí, en algo!… en los dos repartís y también restás… Maestra: ¿Se parecen o no? Leo dijo que nada que ver… Cristian O: Sí se parecen porque… porque… ¿cómo sería?… sería que podés decir “Joaquín tiene $389 y gasta 6 por día ¿Cuántos días comés?”. Es lo mismo. Maestra: Entonces como dice Cris, uno se podría transformar en el otro y haríamos los mismos cálculos, ¿no?… Walter: ¡Son de repartir también! Porque ves todos los 6 que podés repartir. Maestra: Claro, ¿entienden lo que dijo Walter? Estos problemas, en los que veo cuántas veces puedo sacar un número o cuántas veces entra un número en otro, son problemas de dividir. También de resta, pero para hacerlos de una manera más corta se puede dividir. |
En este caso, la intervención de la docente apunta a relacionar dos problemas que tienen un sentido similar –ninguno de los dos explicita un reparto–, pero tienen contextos muy diferentes.
|
Para resolver problemas es importante poder entender bien de qué se trata la situación:
|
O carteles que expliciten lo que hay que tener en cuenta para que la resolución de un problema esté completa:

Frente a soluciones erróneas, por ejemplo porque el niño elige una operación incorrecta o porque usa todos los números del enunciado (aun los que no son pertinentes), se puede:
- Analizar juntos la función que cumple la información que se da en el problema, identificar qué información sirve y cuál no para la pregunta planteada. Por ejemplo: ¿Qué es ese 15 en el problema? ¿Son cajas o libros? Se trata de analizar que no toda la información que brinda el problema resulta un dato para su resolución.
- Determinar si el resultado obtenido resulta razonable en el contexto del problema planteado. Por ejemplo: ¿Puede ser que puedan armarse 450 filas si hay 287 sillas en total?
Otras sugerencias posibles para el trabajo en el aula con problemas son:
- Variar las palabras que se utilizan en los enunciados para que la decisión de qué procedimiento usar no quede “atada” al vocabulario empleado. Por ejemplo, en situaciones de división debe cuidarse de no usar siempre “repartir”, o de usar “repartir” en situaciones que no se resuelven con una división.
- Ante un niño que muestra dificultades con problemas que abordan sentidos más complejos de una operación, plantear otros problemas con sentidos más sencillos para conocer si en ese caso puede resolverlos. Si tampoco puede resolverlos, será necesario priorizar y destinar tiempo al trabajo sobre ellos. Si puede resolverlos, se tratará de ayudarlo a establecer vínculos entre estos y otros más complejos, para ampliar los sentidos asociados a una operación.
- Incorporar en la secuencia de actividades destinada a la enseñanza de una operación algunos problemas que no se resuelvan con esa operación. Esto puede permitir que los niños analicen cada situación y tomen decisiones y no que, por ejemplo, decidan hacer una división solamente porque estamos aprendiendo a dividir.
- Indicar el uso de la calculadora para resolver problemas. Si la intención de la enseñanza está centrada en analizar problemas para decidir qué operación/es podría/n resolverlos, se puede pedir que, una vez decididos los procedimientos se use la calculadora para encontrar la respuesta. Esto permite que la atención se concentre en la comprensión de la situación planteada y no en cómo efectuar el cálculo.
- Variar las formas en las que se presenta la información incorporando diversos soportes: tablas, gráficos o imágenes. Aprender a interpretar la información disponible en cada formato requiere intervenciones específicas del docente.
El caso de los problemas de proporcionalidad
En el segundo ciclo ocupa un lugar central el trabajo con problemas de proporcionalidad. Al plantear su enseñanza, es necesario tener en cuenta que la proporcionalidad se inscribe en el campo de lo multiplicativo, e implica un conjunto de conceptos relacionados, que se adquieren simultáneamente durante un período prolongado de tiempo. El aprendizaje de este contenido, como sucede también con otros centrales del ciclo, no termina en la escuela primaria. En la escuela secundaria será retomado y resignificado.
A lo largo del ciclo se pueden plantear problemas de diversa complejidad. Esa variación en la complejidad está dada, entre otras cuestiones, por:
- los tipos de números en juego (naturales, fraccionarios o decimales);
- la naturaleza de las magnitudes intervinientes: continuas (longitud, peso, área, volumen, velocidad) o discretas;
- las relaciones entre unidades de medida involucradas;
- los casos particulares de su utilización: porcentaje, escalas, velocidad;
- el tipo de tarea;
- la forma de presentación de la información.
A partir del trabajo con situaciones de proporcionalidad se espera que, por un lado, los niños puedan identificar cuál es el tipo de vínculo que hay entre las magnitudes que se relacionan proporcionalmente y por lo tanto puedan reconocer cuándo dos magnitudes son proporcionales o no; y por otro lado, que puedan entonces, en situaciones de proporcionalidad, encontrar nuevos valores a partir de otros dados, poniendo en juego la constante de proporcionalidad o las propiedades que caracterizan a esa relación:
- al duplicar, triplicar, etcétera, o al calcular la mitad, tercio, etcétera, de la cantidad inicial de una magnitud también se duplica, triplica o se calcula la mitad, tercio de la otra;
- al sumar dos valores de una de las magnitudes, corresponde sumar los valores correspondientes a cada uno de la otra magnitud;
- existe una relación multiplicativa constante entre las dos magnitudes. Hay un valor constante que es el cociente entre los valores de ambas magnitudes.
Algunas consideraciones para tener en cuenta:
- Es necesario presentar problemas con enunciados textuales y, también otros, con la información organizada en tablas de valores. Las tablas son una forma de organizar los datos que permite identificar mejor las relaciones en juego entre ellos. Es necesario que los niños aprendan a leer la información contenida en una tabla (cuestión que muchas veces no es sencilla ni evidente) y aprendan también a elaborar tablas a partir de problemas enunciados como texto.
- Un aspecto valioso del trabajo con este contenido es la posibilidad de desplegar diversos procedimientos para resolver las situaciones planteadas, según los números involucrados. Se espera que los niños accedan a diferentes formas de resolverlas.
- El tipo de procedimiento más pertinente para resolver una situación y, por lo tanto, las
relaciones que se pueden analizar, dependen de los números considerados. Es importante
que se tenga en cuenta esto a la hora de diseñar o elegir situaciones de enseñanza:
- Puede incluirse o no el valor de la unidad (la constante de proporcionalidad). Si el valor de la unidad está dado, el problema resulta más sencillo, pues se puede utilizar ese valor para encontrar todos los otros valores.
- Los datos pueden estar ordenados de forma creciente y consecutiva o no.
- Los datos pueden permitir o no que se pongan en juego las relaciones de dobles, triples, mitades, etc.
- Si no se incluye el valor unitario, se podría calcular de diversas formas, según qué datos se den. Por ejemplo, puede calcularse dividiendo el valor de una magnitud por el correspondiente de la otra magnitud, o buscando la diferencia entre dos valores consecutivos de una misma magnitud. Por ejemplo, en la tabla que sigue se podría averiguar que un cuaderno cuesta $84 ya que es la diferencia entre el valor de 12 cuadernos y el de 13 cuadernos, o sea 1.092 – 1.008 = 84.
Cantidad de cuadernos 12 13 14 Precio (en $) 1.008 1.092 …… - Puede ser un buen recurso incluir en las tablas algunas columnas vacías para que los alumnos completen, a partir de la propuesta del maestro, con valores intermedios que resulten de apoyo para encontrar los valores pedidos. Por ejemplo, en la siguiente tabla, podría ser útil encontrar el valor de 2 cajas para sumar ese valor con el correspondiente a las 7 cajas y así obtener el de 9 cajas. También podría encontrarse el valor de una caja.
- Es necesario explicitar con los niños la relación entre la proporcionalidad y otros conceptos sobre los que los niños irán trabajando a largo del segundo ciclo. Es central que los alumnos construyan la idea de porcentaje como una relación de proporcionalidad, en la que la cantidad de referencia es 100. También es necesario reflexionar sobre las relaciones de proporcionalidad involucradas cuando se pasa una medida dada en una unidad a otra unidad (una longitud, por ejemplo). En ese caso la medida de una longitud en una unidad determinada, por ejemplo, centímetros, es proporcional a esa misma medida expresada en otra unidad, por ejemplo, decímetros.
- También es necesario proponer a los alumnos situaciones en las que deban analizar si en los problemas dados las magnitudes se relacionan o no proporcionalmente. Esto es una oportunidad más para volver a sistematizar las propiedades que caracterizan el modelo de la proporcionalidad. Es importante que los alumnos avancen en poder determinar si una relación entre magnitudes es de proporcionalidad directa o no, cuáles de sus características son necesarias pero no alcanzan para estar seguros y cuáles son suficientes.
| Cantidad de cajas | 4 | 7 | 8 | 9 | ||
| Cuadernos | 192 | 336 | …… | …… |
- GCABA, Ministerio de Educación (2017) Matemática. 2º ciclo. Primera parte. Material para el alumno. Aceleración y Nivelación. Serie Trayectorias Escolares. Consultar »
- GCABA, Ministerio de Educación, DGPLEDU, Dirección de Currícula y Enseñanza (2012) Diseño Curricular para la Escuela Primaria. Primer ciclo. 1ª reimp., pp. 318-328. Consultar »
- Ministerio de Educación de Nación. Matemática. Para seguir aprendiendo. Tareas de acompañamiento para alumnos y alumnas de 4º y 5º grado. Cuadernillo de actividades. Serie Aprender con todos. Consultar »
- Ministerio de Educación, Ciencia y Tecnología de la Nación (2007) NAP. Matemática 4, 5 y 6. Segundo ciclo EGB / Nivel Primario. Serie Cuadernos para el aula. 4º grado: pp. 113-117, 5º grado: pp. 113-117 y 6º grado: pp. 112-121. Consultar »